A MONSTER THAT CALCULATES WHAT MAN DOES NOT UNDERSTAND

Modern life is closely linked to computers. But classic computer technology has already largely reached its limits. Scientists are therefore looking for new directions that could make a revolutionary breakthrough in computing. The most promising is considered to be the quantum computer, which should be much more efficient than anything that has been created so far[1] .
It is such a complex computer that it is difficult to understand it because it no longer uses the binary system (where there are very long series of 0s and 1s which make up, thrown at breakneck speed, the sequences describing reality and motion) but the quantum system, which is three-dimensional: if in arithmetic one plus one gives two, then if you want to make a quantum calculation, then you must add to 2 all the positions occupied in space by the energy source that triggered the question and those from which the answer came. So one plus one gives a different result each time. And this is where things get interesting, frightening, disturbing.
Because we are entering a world in which an object that is fundamental to our survival can no longer be repaired by humans. The day we decide to use a quantum computer or endow our home with the ability to control ourselves according to the principles of quantum physics, we will have to rely entirely on artificial intelligence – the only one capable of understanding and repairing such complex systems. You don’t have to watch a science fiction movie to fear a change of this magnitude.
A new type of particle in the universe

Higgs boson[2]
We live in a three-dimensional world in which everything is explained by the laws of physics and, if you take our world apart, there are only two types of particles: “fermions”, which repel each other, and “bosons”, which like to stick together. Moving energy and static energy, in short. A well-known example of a fermion is an electron carrying electricity, and a well-known boson is a photon carrying light. But if we look at the two-dimensional world, where particles can rotate around each other in only two different ways (clockwise or counter-clockwise), we find another type of particle – anions, which behave neither like fermions nor bosons and interact somewhere between attraction and repulsion. Their existence was first announced in the late 1970s as a logical hypothesis, but experimental proof of their existence was not obtained until 2020 .[3]
Anions are charged particles that are formed when an atom or group of atoms receives one or more additional negative charges. Atoms are made up of protons (positively charged), neutrons (uncharged) and electrons (negatively charged). In a neutral atom, the number of protons is equal to the number of electrons, which guarantees its neutrality. However, when an atom or group of atoms acquires one or more extra electrons, anions are formed[4] .
The existence of anions has been demonstrated by a team of French scientists. They have created a tiny two-dimensional collider in which charged particles move like in a crossroads with four paths, with two entrances and two exits[5] . If you send “similar” bosons along two inner paths, they will meet at the crossroads and then exit together along the same path. However, if you send charged particles with an extra negative charge, they behave quite differently: sometimes they come together, sometimes they don’t. Although they tend to cluster together as bosons, the exact degree of closeness lies in their vibrational nature, which is the measure that ultimately determines the calculation[6] . That is, instead of there being only one possible solution, there is an almost infinite number of possible solutions.
Anions obey an unusual rule of exchange: in two-dimensional space an exchange of the same particles twice is not equivalent to an exchange without them (- x – ≠ +), because the position of the particles after the exchange twice may be different from the initial one. This process of exchanging the same particles or rotating one particle around the other is called “entanglement”. The “entanglement” of two anions creates a historical record of the event[7] , as their changed wave functions “count” the number of entangled particles[8] .
If we consider these “quasi-particles” in terms of mathematical group theory, the anions can be divided into “abelian” and “non-Abelian”, depending on the properties of their behaviour in the group. An Abelian group (or commutative group[9] ) is a group in which the order of the elements in the operation does not matter. A non-Abelian group is a group in which the order of the elements in the operation is important. If the anions A and B are non-Abelian, then generally speaking A + B ≠ B + A. In other words, not only the particles themselves, but also the sequences of their motions and mutations must be counted[10] . A calculation with an insane number of variables, such that it cannot be realistically controlled by humans, and whose results contradict everything we thought we knew, and yet are true[11] .
Classical versus quantum

The Wall of Dominance, the first quantum object ever created in a laboratory[12]
Non-Abelian anions (or non-abelian anions) are of interest for quantum physics because their properties allow quantum calculations based on topological order. Non-Abelian topological order is a desirable state of matter with remarkable properties[13] , including the existence of “quasiparticles” which can remember the sequence in which they oscillate. Their entanglements are the so-called qubits, the basis of the quantum computer[14] . They are promising building blocks for fault-tolerant quantum computers, as they become predictable after sufficient observation[15] . In addition, phenomena such as quantum coherence (coherence of motion of microparticles forming a given physical system[16] ) and quantum dependence (a quantum mechanical phenomenon[17] , in which quantum states of two or more objects appear interdependent even after separation)[18] are associated with non-Abelian elements.
A quantum object is an object in a microcosm, and therefore very small: the microcosm is a world of objects so small that they cannot be directly observed with the naked eye (molecules, atoms, elementary particles), and it functions differently from the world we are used to: a world in which probability is the cornerstone and the object state cannot be clearly defined, because its own laws and rules apply there .[19]
Thus, the differences between conventional (classical) and quantum computers start immediately with fundamentally different information processing systems. Conventional computers use binary digits to represent and process information. A bit is a minimum value of information, which can have a value of 0 or 1. Quantum computers, on the other hand, use quantum bits – qubits – which can be in states 0 and 1 simultaneously[20] . This is due to the nature of quantum mechanics, in which objects can exist in all possible states simultaneously, which is called superposition[21] .
The principle of quantum superposition is perfectly illustrated by the classic example of Schrödinger’s cat. Let’s imagine a closed vault, inside which there is an ordinary cat and a hell machine protected by it. Inside the infernal machine there are very few radioactive atoms. And the probability that at least one of them will decay in one hour is equal to the probability that none of them will decay, i.e. 50:50. Around the radioactive material there is an electron sensitive screen.
If even one atom disintegrates, a mechanism is triggered that releases a poisonous gas and the cat dies. We can’t accurately predict whether the cat is dead or alive. To do that, we have to open the safe and look. And when it is closed, the cat is superimposed: it is both alive and dead[22] . If we open and close the door several times, we get to the point where we have so many equally possible variables that we go crazy. This example illustrates one of the principles of the quantum world: the ability of a quantum particle to be in all states simultaneously until the experimenter makes an observation – instantaneous fixation of the momentary state.
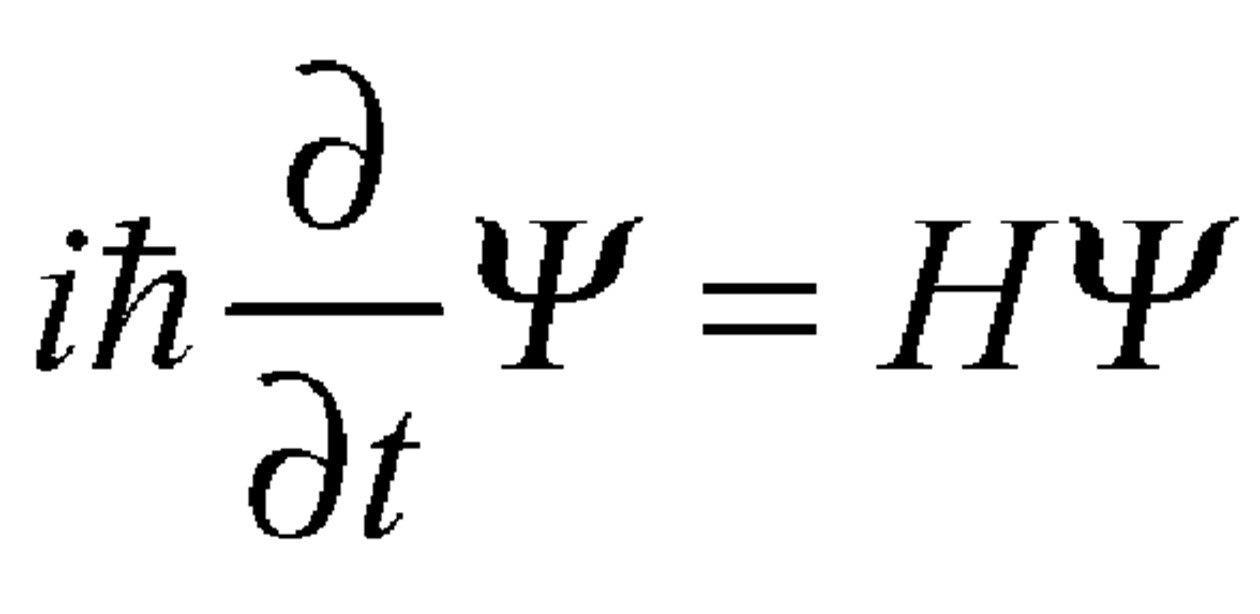
Erwin Schrödinger’s equation, which in 1927 managed to calculate the oscillation of particles in space, surpassing Einstein’s innovations[23]
In classical computers, information is processed sequentially using conventionally simple actions such as addition, multiplication, logical operations, etc. Quantum computers can process information in parallel thanks to quantum superposition. This is not a well-defined quantity, but the probability of getting one of these states. For example 3 bits of information can give one of eight combinations of zeros and ones: 000, 001, 010, 100, 011, 101, 110, 111. Cubits operate with eight possible combinations at the same time, calculating probabilities rather than explicit values. And with each qubit the processing power grows exponentially: 10 qubits can simultaneously operate on 1024 combinations and 30 qubits can operate on more than 1 billion[24] . This allows certain operations to be carried out much faster.
In conventional computers, information is processed using electrical signals represented as voltage or current. Quantum computers operate on the basis of quantum phenomena, which require special equipment and environmental controls because nanoscale particles are very sensitive to external influences and quantum states are not always stable.
Conventional computers handle many tasks well, such as word processing, computing, data management and so on, while quantum computers have the potential to solve some tasks that are difficult or impossible with classical computers, such as factorisation of large numbers, optimisation, modelling of complex systems and development of new materials. There are many promising fields for the quantum computer, such as molecular biology and genetics, neuroscience and artificial intelligence, cryptography and others[25] . Wherever probability prevails over clarity, the quantum computer could play a key role.
Quantum problems
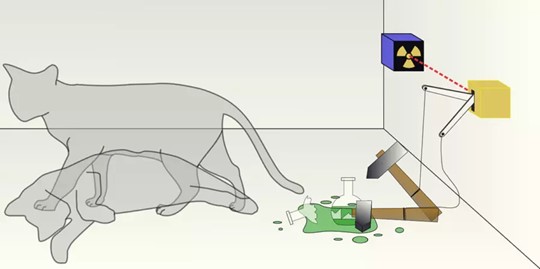
Graphic illustration of the Schrodinger’s cat experiment[26]
Although the world has already decided that a quantum computer is necessary, the question of its stability remains open. The creation and use of a topological quantum state could revolutionise everything. Non-beleons have a unique and useful property: they remember part of their history. This “memory” of non-Abelion can be represented as a continuous straight line in space-time. When two nonabeleons swap places, the lines of their movement intersect. If wound properly, the resulting knots and braids form the basic operations of a topological quantum computer – and that is why they are so valuable: because they accelerate our ability to compute[27] in an important way.
The creation of topological quantum states strongly depends on the strength of interactions between qubits, the units of information. As more qubits are added to the system, the interactions between them become increasingly complex, making it difficult to maintain topological protection, that is, a state in which the system will be stable even in the presence of external perturbations such as noise or defects[28] . But creating, manipulating and doing useful things with nonablions in a quantum computer is difficult. The more variants come into play, the more incoherent information is pulled into the overall computation, and thus the level of complexity increases.
A team of physicists from the Quantinum, California Institute of Technology and Harvard University used a quantum computer to create virtual particles and move them so that their paths form a Borromean ring – a grid of three topological circles in which two of the three rings are not connected (i.e. if you remove one ring, the remaining two rings disconnect)[29] . Important detail: if they are disconnected, not only does the computer not shut down, but it continues to seek order in chaos undauntedly – it is simply out of human control[30] .
In the experiment, the scientists used the company’s most advanced machine, called H2, equipped with a chip that can create electric fields to trap 32 ions of the element ytterbium on its surface. Each ion can encode a cubit, a unit of quantum computation that can be either “0” or “1”, like normal bits, or a superposition of both states simultaneously. These ions are entangled in a kagome-like lattice – a mosaic of regular triangles and hexagons surrounding each other – and all particles have the same quantum state.
The entangled states, in the two-dimensional virtual universe of simplest arithmetic, do not move energy – in fact, they are states in which there are no moving particles. But by further manipulation, the mosaic we call kagome can be translated into excited states[31] – that is, it can easily be turned into a space in which photons, driven by acceleration or heat, collide and create impressive amounts of energy[32] . This corresponds to the appearance of particles which must have the properties of non-Abelian particles (which refuse to order themselves into predetermined tracks).
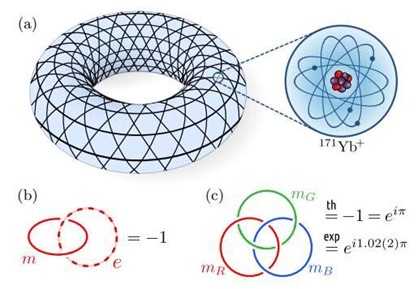
Creating and managing non-Abelian wave functions[33]
To prove that excited states are non-Abelian, scientists have carried out a number of tests. The most convincing of these involves moving excited states to create virtual borromine rings[34] . The appearance of the model confirms the movement and measurements of ions[35] . The quantum approach has the advantage that, compared to most other types of qubits, the ions are trapped and can be moved and forced to interact with each other, allowing quantum computers to perform calculations[36] .
This experiment was a physical simulation of non-Abelian anions in action, which showed that they could be a stable basis for quantum computing[37] . Scientists at Google Quantum AI have shown that it is possible to correct for the loss of quantum information due to the disruption of qubit coupling that occurs when a quantum mechanical system interacts with its environment using non-Abelian anions.
In the new study, the role of non-Abelian anions was calculated from the number of defects in the surface code (which combines several physical qubits into one logical code and is therefore easier to design) represented as a square graph (mathematical model of the system)[38] . The defects were topological in nature and thus had the right properties to simplify the square graph[39] . The study showed that by moving the defects along the graph, it was possible to weave and encode quantum information in this way. Thus, physicists have demonstrated that neabelion-based logic qubits in a superconducting quantum processor are potentially suitable for quantum computing[40] .
Non-Abelian anions and their statistical properties have potential importance in various fields of science and technology. The most desirable area of application of their unique properties is quantum computing, where the topological quantum states of non-Abelian anions can create more powerful and stable quantum computers capable of solving complex problems beyond the capabilities of their classical counterparts. In addition, nonabelian anions are theoretically capable of making important contributions to the transmission, storage and coding of quantum information.
Neabelions are also studied in the context of quantum gravity and string theory[41] . Their properties may help to understand quantum aspects of gravitational phenomena and find a unification of quantum physics and gravity theory[42] . Non-Abelian states are some of the most complex quantum states that exist in theory and hold promise for new types of quantum information processing. The fact that these states can be precisely prepared and controlled is a testament to the rapid development of quantum devices over the last decade and opens up a number of new questions[43] .
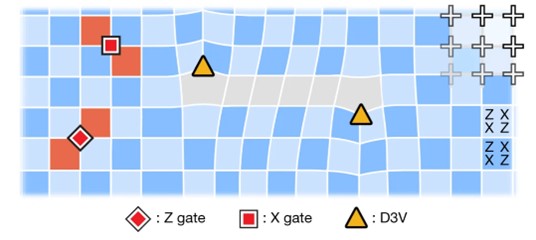
A graph representing the surface code on a grid of physical qubits (plus). The yellow triangles are the defects responsible for the formation of non-abelianity[44] .
The fact that their existence has been proven represents a breakthrough for quantum science. Neabelions could become a tool to search for exotic states of matter, which until now have remained a far-fetched idea in physicists’ theories[45] . These are concepts that are difficult to explain, but which profoundly affect our life system: classical computers and even spacecraft that have reached the Moon and Mars operate on the basis of a binary system: there are only “on” and “off” ordered in very long sequences to represent the entire real world. It’s a slow, faulty system, which in some situations makes the universe, which is not binary, behave like a video game from half a century ago.
Quantum mechanics tries to calculate the universe as it is, and for that reason d we need to be able to predict the unpredictable, look for repetition where there used to be rules, probabilities where there used to be certainty. Our computers, both analogue and digital, force the world into simplicity. Quantum computers do not. Not only that: they learn autonomously and are capable of storing immeasurable amounts of data in their memory. If you don’t hit the axe, only a quantum computer can fix a quantum computer.
The development of all this is obvious: the quantum will bring us closer to the stars, but it will do so on its own – we will only be spectators, all involved in understanding what the quantum computer has discovered, analysed, evaluated, decided, converted into useful knowledge for later discoveries. We have opened Pandora’s box.
USA025
[1] https://scientificrussia.ru/articles/osnova-dlia-kvantovogo-kompiutera
[2] https://www.geopop.it/cosa-sono-i-bosoni-e-quali-sono-i-principali-tipi-spiegato-in-modo-semplice/
[3] https://sciencex.com/wire-news/347971706/finally-anyons-reveal-their-exotic-quantum-properties.html
[4] https://new-science.ru/anion/
[5] When a particle meets its antiparticle, both annihilate, releasing pure energy. After World War II, scientists built colliders – machines that accelerate protons until they collide and release energy. In 1960, Austrian physicist Bruno Tuschek came up with the idea of using accelerators to make matter and antimatter collide. Today there are extremely complex examples of this, in which protons collide (and gather energy) with antiprotons – httpshttps://scienzapertutti.infn.it/7-collisorescienzapertutti.infn.it/7-collisore .
[6] https://phys.org/news/2020-04-anyon-evidence-tiny-collider.html
[7] https://phys.org/news/2020-07-evidence-anyons.html
[8] The entanglement of two particles is an extraordinary relationship that binds them together independently of any obvious rules and cannot be predicted. The moment we observe the motion of particles, we find that two or more of them are moving along each other’s lines – and so they are entangled. It is not clear how this is possible, because the associated motions are faster than the speed of light, and therefore any transfer of information between two particles is impossible. For an observer, the more particles are entangled, the more predictable the behaviour of the system. We don’t know why, but we know how – httpshttps://www.geopop.it/una-spiegazione-semplice-dellentanglement-quantistico/www.geopop.it/una-spiegazione-semplice-dellentanglement-quantistico/ .
[9] Arithmetic is a commutative group because the result of the calculation remains the same even if the coefficients are reversed: for example, 2+1 always has the same result as 1+2 – https://www.andreaminini.org/matematica/gruppi/gruppo-abeliano
[10] https://nplus1.ru/news/2023/05/16/non-abelian-anyons
[11] https://www.wired.it/scienza/spazio/2020/01/30/fenomeni-strambi-mondo-quantistico/ ; https://w3.lnf.infn.it/levoluzione-parallela-fisica-matematica/
[12] https://www.tomshw.it/scienze/un-oggetto-quantistico-e-stato-creato-per-la-prima-volta-in-laboratorio/
[13] Topological sorting is a term taken from geometry, i.e. graph theory, which seeks to define systems which obviously are not – thus it seeks to recognise the possible behaviour of certain matter which obviously have nothing to do with each other and instead appear to be synchronously interacting. In our case, the predictability of the 1 + 1 result in the quantum dimension is ensured by locating in the three-dimensional field all the positions occupied by 1 + 1 – httpshttps://en.wikipedia.org/wiki/Topological_sortingen.wikipedia.org/wiki/Topological_sorting ; https://en.wikipedia.org/wiki/Graph_theory.
[14] https://www.focus.it/scienza/scienze/entanglement-quantistico-intervista-spiegazione
[15] https://arxiv.org/abs/2305.03766
[16] Quantum coherence is based on the idea that all objects have wave properties. It is in many ways similar to the concept of quantum entanglement, which implies common states of two quantum particles instead of two quantum waves of one particle. If the wave properties of different particles or quasiparticles are the same (and therefore superimposed on each other), this is called quantum coherence – httpshttps://it.theastrologypage.com/quantum-coherenceit.theastrologypage.com/quantum-coherence .
[17] This is a difficult concept to grasp, and it has to do with a human error of perception of reality. Let me try to explain: if a man suffers from thirst in the desert, he desperately dreams of finding water. If he finds it and has to drink to quench his thirst, he risks dying, because he has confused one of his projections of reality (the need for water) with quantum dependence (the body needs the balance between water and body matter, and if this balance is broken, it has to be restored in the body, starting with the skin, not in the stomach, which needs too long to turn the water it drinks into the water it needs – httpshttps://lifeshifting.it/2018/05/11/2223/lifeshifting.it/2018/05/11/2223/ ; https://tech.everyeye.it/notizie/numeri-immaginari-indispensabili-descrivere-realta-561343.html ; httpshttps://www.sciencedirect.com/science/article/pii/S0550321322000426www.sciencedirect.com/science/article/pii/S0550321322000426 ; https://www.nature.com/articles/s41535-023-00540-3) .
[18] https://www.europeantimes.news/ru/2023/04/physicists-take-a-step-toward-fault-tolerant-quantum-computing/
[19] https://2051.vision/2023/04/08/chto-takoe-kvantovyy-kompyuter-i-kak-on-rabotaet/
[20] As we have explained, even the simplest addition (1+1) has one result in the two-dimensional world of arithmetic, whereas in the quantum world, which is three-dimensional, 1+1 can have many results, and qubits are the units by which we measure the huge number of possible results that even the simplest arithmetic addition gives in the quantum world – httpshttps://en.wikipedia.org/wiki/Qubiten.wikipedia.org/wiki/Qubit .
[21] https://2051.vision/2023/04/08/chto-takoe-kvantovyy-kompyuter-i-kak-on-rabotaet/
[22] https://habr.com/ru/companies/bigdataplatform/articles/681332/
[23] https://www.corriere.it/scuola/universita/test-ammissione-preparazione-e-orientamento/cards/sono-17-equazioni-che-hanno-cambiato-mondo-quante-ne-sapete/equazione-schroedinger.shtml
[24] https://habr.com/ru/companies/bigdataplatform/articles/681332/
[25] https://habr.com/ru/companies/bigdataplatform/articles/681332/
[26] https://vc.ru/future/548157-kvantovyy-kompyuter-chto-zachem-kogda
[27] https://phys.org/news/2023-05-google-quantum-ai-braids-non-abelian.html
[28] https://www.youtube.com/watch?v=O5Kv3j06oF8
[29] https://phys.org/news/2023-05-nonabelions-quantum-prone-errors.amp
[30] https://cordis.europa.eu/article/id/153918-homotopy-theory-of-higher-categories/it
[31] https://www.google.com/search?client=firefox-b-d&q=kagome+states+excited#ip=1
[32] https://www.chimica-online.it/download/stato-eccitato.htm
[33] https://phys.org/news/2023-05-nonabelions-quantum-prone-errors.html
[34] https://www.zerounoweb.it/analytics/cognitive-computing/quantum-error-scoperte-nuove-particelle-che-danno-speranza/ ; https://www.cmic.polimi.it/magazine/molecular-sciences/nodo-borromeo-supramolecolare-studio-pubblicato-su-chem/ ; https://www.lescienze.it/news/2023/05/16/news/anyoni_nonabelioni_calcolo_qubit_topologici_resistenza_errori-12092348/
[35] https://www.nature.com/articles/d41586-023-01574-0
[36] https://www.nature.com/articles/d41586-023-01574-0
[37] https://arxiv.org/pdf/2305.03766.pdf
[38] http://pages.di.unipi.it/mastroeni/mod/Modelli_su_grafi1.pdf
[39] It is a complex concept: differential equations try to estimate the value of some initially unknown quantity, e.g. x and y. It is a simple principle that, when applied, becomes increasingly complex. It happens that, in unravelling a very complex equation, one realises that there are parts of the equation that graphically overlap and hence are called topological defects and can be ‘simplified’ two by two, with a large reduction in overall complexity. This is even more true in the quantum domain, where the equations are three-dimensional – https://reccom.org/difetto-topologico-rottura-spontanea-della-simmetria/ .
[40] https://nplus1.ru/news/2023/05/16/non-abelian-anyons
[41] Simply put: non-abelions contribute to the simplification of quantum computation and hence to the representation of complex computation, which is easier to solve because of their existence
[42] The theory of general relativity, created by Newton and refined by Einstein, uses two-dimensional calculations and solves problems arising from the concept of curvature of space. Today, quantum physics is trying to develop a theory of gravity that takes into account all that we have learned from quantum physics. The most famous development of this research is the so-called “string theory”, which suggests that some qubits can be represented, due to their motion, not as points, but as strings. – httpshttps://www.treccani.it/enciclopedia/gravita-quantistica_%28XXI-Secolo%29/www.treccani.it/enciclopedia/gravita-quantistica_%28XXI-Secolo%29/ ; https://plato.stanford.edu/entries/quantum-gravity/ ; https://www.treccani.it/enciclopedia/gravita-quantistica_%28Lessico-del-XXI-Secolo%29/ ; https://plato.stanford.edu/entries/qm-relational/
[43] https://arxiv.org/pdf/2305.03766.pdf
[44] https://nplus1.ru/news/2023/05/16/non-abelian-anyons
[45] In thousands of experiments conducted around the world to improve quantum theory, scientists have realised that there are moments when highly refined crystal structures are born and then die, whose decay is due to the fact that the particles that make them up are ephemeral (i.e. they only exist for a few seconds and then change). These particles are called “excitons” and the analysis of their phenomenology is called the study of “exotic states” of matter – https://it.dayfr.com/tecnologia/436185.html ; https://www.wired.it/scienza/lab/2016/10/04/materia-esotica-nobel-fisica/ ; https://reccom.org/scoperto-un-nuovo-stato-esotico-della-materia/ .




Leave a Reply